FOUNDATIONS OF MACHINE LEARNING
Course info
Course materials
FAQ
Course materials
/
Section
Predicting Apartment Prices
The real estate agency LinkLiving has many years of experience of selling apartments in the city of Linköping. After all these sales they have acquired a large dataset of apartments they have sold. The dataset includes different properties of each apartment, as well as the final price of the sale. LinkLiving have now asked you to apply your machine learning skills on this dataset. They want a model that can predict the final selling price based on different properties of an apartment. With such a model LinkLiving could quickly give new customers who want to sell their apartments an estimate of what the final price would be.
Using their experience of the housing market, the agency have adjusted the apartment prices in the dataset both for inflation and the general fluctuations of the market. This means that you can assume that the sales price only depends on properties of the apartment itself. LinkLiving’s dataset contains the following attributes associated with each apartment:
- Size [m$^2$] - Total floor area
- Age [years] - Years since the apartment was constructed
- Street (Storgatan/Rydsvägen/…) - Street the apartment is on
- Rooms - Number of rooms in the apartment
- Distance to city center [m] - Distance to the city center of Linköping
- Balcony (yes/no) - Whether the apartment has a balcony
Each apartment additionally has a sales price attribute, which is what you want to predict.
What type of problem is the apartment price prediction?
Which of the apartment attributes described above are numerical?
To build and evaluate a first model you choose to only work with two of the attributes in the dataset. The real estate agents at LinkLiving believe that the size of an apartment and how centrally it is located (distance to city centre) are the most important attributes for determining the price. Following their advice, you decide on using these two attributes in your model.
You extract the size attribute (size) and distance to city center (center_dist) together with the price (price) from the dataset.
In the table below are some examples of apartments in the dataset.
index |
size |
center_dist |
price |
|---|---|---|---|
| 0 | 91 | 1 686 | 3 574 000 |
| 1 | 86 | 2 666 | 3 123 000 |
| 2 | 38 | 2 711 | 2 080 000 |
| 3 | 80 | 2 446 | 3 533 000 |
| 4 | 71 | 4 811 | 2 253 000 |
| 5 | 85 | 1 884 | 3 764 000 |
| 6 | 36 | 1 746 | 1 886 000 |
| 7 | 38 | 1 847 | 1 703 000 |
| 8 | 24 | 1 627 | 1 315 000 |
| 9 | 58 | 4 439 | 2 287 000 |
You divide the entire dataset into training data and validation data. Doing so, you end up with 200 training data points and 100 validation data points.
Training, Test and Validation data
As you have seen before, training data is what we use in the training process to learn our model. To later evaluate the learned model we use a set of held-out test data. Often it is useful to consider a third set of data, validation data. Validation data is also held-out from the training process, just like test data. The difference is that we can use validation data when deciding hyperparameters for our model, like the value of k for k-NN. These different sets of data, how they can be extracted from a larger dataset and how they should be used will be discussed more in section 4 of this course.
When possible, it is typically a good idea to plot the data you are working with.
This gives a visual overview and allows for getting a feeling for different properties and relationships between features.
The apartment data contains two features (size and center_dist) as well as a real-valued target variable (price).
In order to visualize all of this we need to use three-dimensional plots.
Plots for three-dimensional Data
Plots of two-dimensional data are very common and we encounter them regularly in everyday life. Visualizing higher-dimensional data in a useful way is however more challenging. There are a few options for plotting three-dimensional data. One straightforward approach is to extend a two-dimensional plot with an additional axis. Such a 3D-plot of the apartment training data can be seen below.
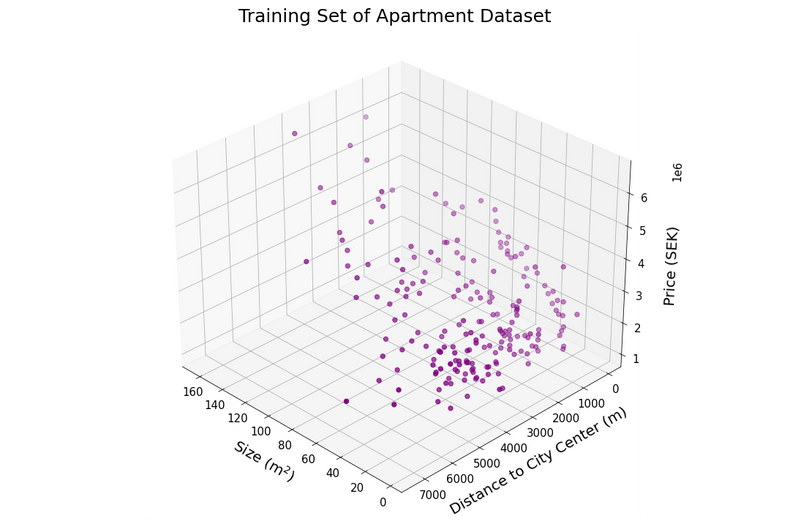
Here the x- and y-coordinates describe the features (size and center_dist), while the price is represented by the z-axis (note that the z-axis has a scaling of $10^6$).
While three-dimensional scatter plots of this type do visualize all information available, they can be quite hard to interpret.
The interpretability often relies heavily on how the axes are rotated to give a good viewing angle.
Another option for visualizing three-dimensional data is to utilize properties like color and size of the points in the figure to represent one dimension of the data. In the figure below the data points are laid out in 2 dimensions, with the features on the x- and y-axis. The price associated with each data point is here represented by color. Decoding the color into a specific value can be done by looking at the color bar at the right side of the plot.
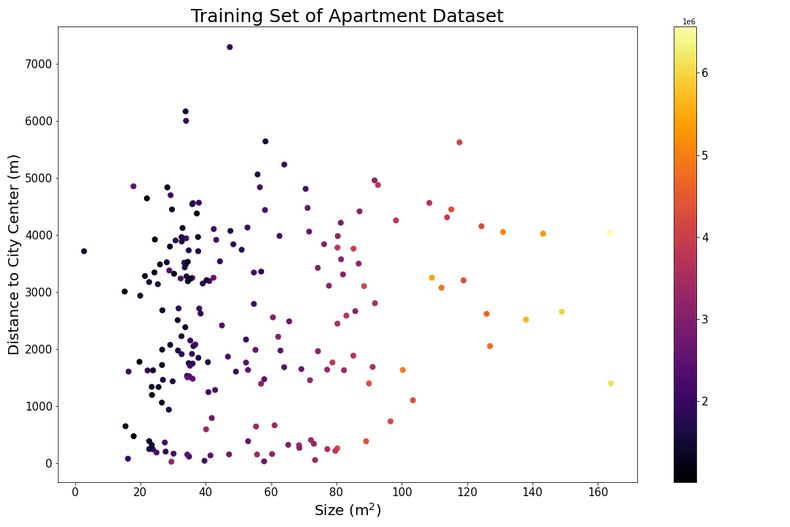
These are two ways of visualizing three-dimensional data, but of course there exist many other techniques as well. Visualizing data in 4 dimensions or even higher becomes a very challenging task. Often we have to resort to plotting only a few feature dimensions at a time.
Scikit-learn and Machine Learning Libraries
Scikit-learn is an open source machine learning library for python. It includes implementations of many of the most common algorithms and models used in modern machine learning. It additionally features useful utilities for data pre-processing and model selection. Scikit-learn uses NumPy for representing vectors and matrices, so most function arguments and return values in the library are NumPy arrays.
To make them easy to work with, models in scikit-learn are implemented following the same pattern.
They have a fit-method for fitting the model to data. fit typically accepts a matrix of feature vectors X and a vector of target values y as arguments.
After the model has been fitted to data, the predict-method can be used to make predictions. predict takes as input another matrix X, containing the feature vectors to make predictions for.
The predictions are returned as a vector.
Preprocessing modules do not produce predictions, but rather transform the data in some way.
They can still have a fit-method, but instead of predict they feature the method transform.
This method takes as input a matrix of samples X and returns a matrix with the transformed samples.
When applying machine learning to real world problems it is typically a good idea to start out by using some existing model implemented in a library. It is often possible to achieve good results by using standard models and tweaking hyperparameters to values suitable for the problem at hand. Sometimes it can be motivated to take the next step and implement a method from scratch. This is typically the case if there is some specific property of the problem that one would want to leverage in the model implementation. It can also be the case that the implementation needs to fit with other pieces of existing software or even run on specific hardware.
In this course we will regularly make use of scikit-learn in the programming questions. We hope that this will make you used to working with a machine learning library to solve different types of problems. It should also give you a starting point for any future machine learning projects that you might work on.
You will here use a k-NN model to solve the problem. To evaluate the model you will need some metric for how good predictions it can produce. Consider the average error in predicted apartment price (in Swedish krona, SEK), computed over the validation data. Mathematically, this corresponds to the so called Mean Absolute Error (MAE). The MAE is computed as
for a dataset $\left\{\mathbf{x}_i, y_i\right\}_{i=1}^{n_v}$ containing $n_v$ validation data points. For example, an MAE of 50 000 in this case means that we should expect price predictions from the model to be wrong by an average 50 000 SEK (too high or too low).
Below you will find some code that loads the apartment dataset.
Fill in the missing parts of the code to make price predictions on the validation set using k-NN.
Use $k=3$.
Compute the MAE of the model based on the predictions on the validation set.
For this task you are recommended to make use of the scikit-learn library, so you do not have to implement k-NN regression yourself.
The neighbors module of scikit-learn contains the KNeighborsRegressor class that is an implementation of k-NN regression.
You can read more about it in the corresponding user guide.
See also the full documentation and an example .
Not completely contempt with your results, you go back and inspect the data again.
This time you realize that the values of size and center_dist are of widely different scale.
This will likely result in poor results using the k-NN model, since different features impact the distances between points differently.
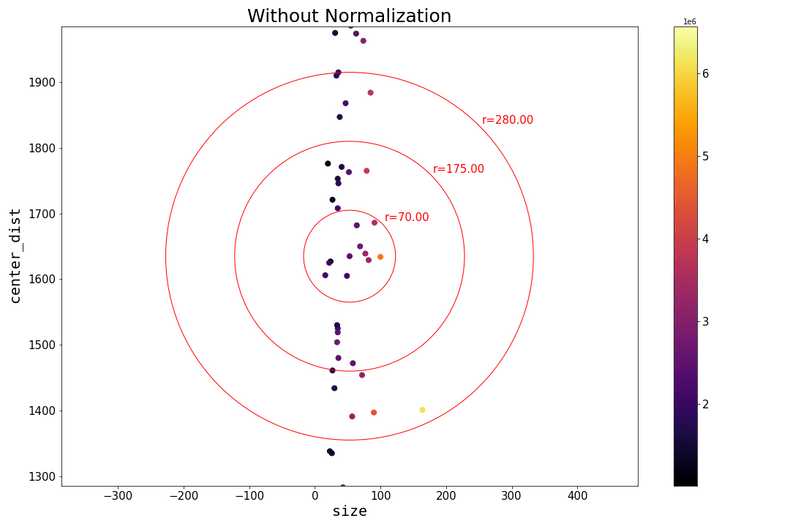
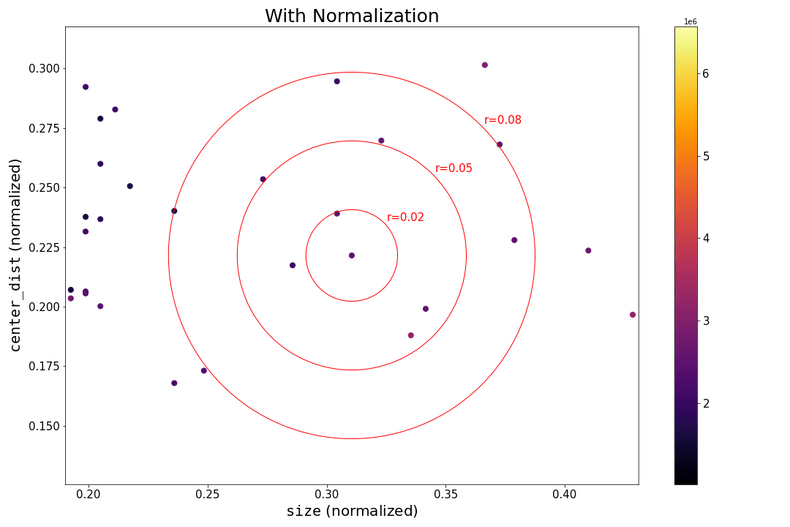
This can be seen in the figures below, where the data has been plotted with the same scaling on both axis.
Without any normalization the size feature hardly impacts the distance from a point to its neighbors.
Whether two data points are close or not is almost exclusively determined by if they have similar center_dist values.
If the data is normalized, as in the second figure, both size and center_dist play a substantial role in determining which are the closest neighbors to a data point.
For a quick and simple normalization method we will here make use of the built-in preprocessing functionality of scikit-learn.
Normalizing data to the range $[0,1]$ can be achieved by using MinMaxScaler (Note that Normalizer in scikit-learn does a different type of pre-processing. Confusing, we know!).
You can read an example of how to use MinMaxScaler here.
Fill in the code below to normalize the training data to the range $[0,1]$. Apply the same pre-processing also to the validation data. Remember to use the same Scaler for the validation data as for the training data. As discussed in the course book, inferring scaling factors separately for validation or test data can lead to incorrect conclusions.
Using your normalized data, apply the k-NN model again. Use k=3. Make predictions for the validation set and compute the MAE. You can reuse code and functions from the earlier questions. Compare your results before and after normalizing the data.
Hopefully the normalization will have resulted in better predictions and a lower MAE. Happy with your improvements, you switch focus to the task of choosing the hyperparameter $k$. Recall that choosing a suitable value of $k$ can be crucial for getting useful predictions from a k-NN model. If we choose $k$ too low the model will overfit to the training data and if we choose $k$ too high the model will be underfitted.
Determine the value of $k$ that gives the lowest MAE on the validation data. You only have to consider $k \leq 20$.
Based on the plot above, the best value for $k$ is:
LinkLiving are very happy with the model that you have created and they immediately want to put it into use. While the k-NN model is simple, it has here shown to be sufficient for the task.
This webpage contains the course materials for the course ETE370 Foundations of Machine Learning.
The content is licensed under Creative Commons Attribution 4.0 International.
Copyright © 2021, Joel Oskarsson, Amanda Olmin & Fredrik Lindsten