FOUNDATIONS OF MACHINE LEARNING

Course info

Course materials

FAQ

Course materials

/

Section

Classifying Horseshoe Bats


Introduction

A team of researchers have dedicated their time to studying bats in southern Europe. They are especially interested in horseshoe bats, a genus of insect eating bats that owe their name to the particular shape of their noses. The researchers have gathered the following data during their time in the field

  • Species (Accuminate/Blasius’s/Guineau)
  • Wingspan [mm]
  • Tail area [mm]
  • Echolocation frequency [Hz]
  • Color of fur (Light brown/Dark brown/Red)
  • Forearm length [mm]
  • Body mass [g]

In total, the research team has observed 1,399 bats.

The team hires you to analyze the data that they have collected. You start your analysis by identifying the properties of the variables in the dataset.


Question A: Variable Types

Which of the variables in the list above are numerical?


Question B: Model Type

The research team is interested in the differences in attributes between the horseshoe bat species. They wish to build a model that can be used to predict the species of a horseshoe bat based on its forearm length and body mass. You are in charge of finding a suitable model.

Would you in this case build a regression or a classification model?

Storing data as arrays

A convient way to store data is using arrays. It is common to store a dataset of the type considered in this exercise in two separate arrays: an input array and an output, or target, array.

As conveyed by the name, the input array is used to store the data that is given as input to the model. In most of the applications that you will encounter in this course, the input array will be two-dimensional. A two-dimensional input array has as many rows as there are observations in the dataset and as many columns as there are input features. Therefore, if we have a dataset with $n$ observations and $p$ features, such an array will be of size $n \times p$. When writing code, we will often refer to the input array by X, sometimes with an accompanying subscript to indicate the intended use of the data. For example, the subscript “train” will often be used to indicate that the data should be used for training.

The array illustrated below represents a subset of four observations from the bat dataset with the features body mass and forearm length included. Each of the four rows of the array represents one single bat and each of the two columns represents one feature. In this case, the columns have been ordered such that the first column of the array contains the body mass of the four bats and the second column contains the forearm length of the bats. Therefore, as an example, the second row of the data array represents a bat with a body mass of 11.8 g and a forearm length of 48.9 mm.

Input array, example
Input array, example

The output array, which we will frequently denote by y in code, is used to store the labels in the dataset. In the bat example, the labels are the species of respective bat and the output array is constructed as illustrated in the figure below. In the figure, the array is shown with the names of the species’ written out explicitly. However, in practice, it is often more convenient (and sometimes required by the models that we work with) to represent the classes with integers in place of strings. In the exercise, we therefore replace the species names with the integers 0, 1 and 2 by performing the following encoding: 0=Accuminate, 1=Blasius’s, 2=Guineau.

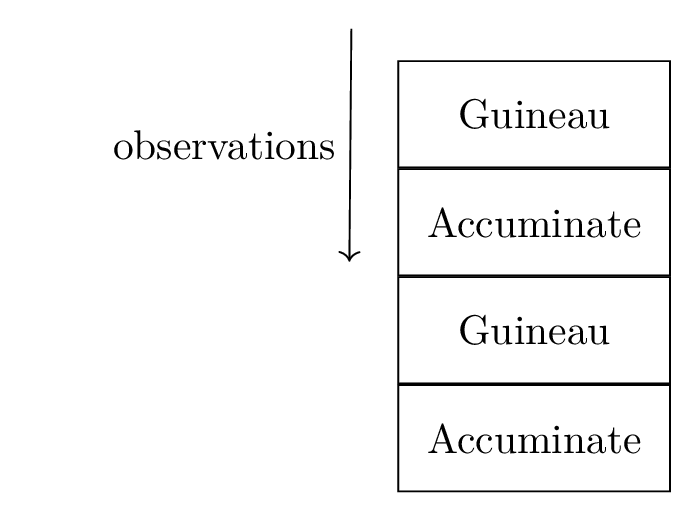
Output array, example
Output array, example

The output array has as many rows as the input array and the species of the bat in the $i^{th}$ row of the input array is given by the $i^{th}$ row of the output array. As an example, the bat with a body mass of 11.8 g and a forearm length of 48.9 mm (second row) belongs to the species Accuminate. Note that although the output array in this example has only one column, this type of array can also have several columns, each representing a different output feature.


Question C: Choosing $k$

We will now apply the k-NN method to the problem introduced above.

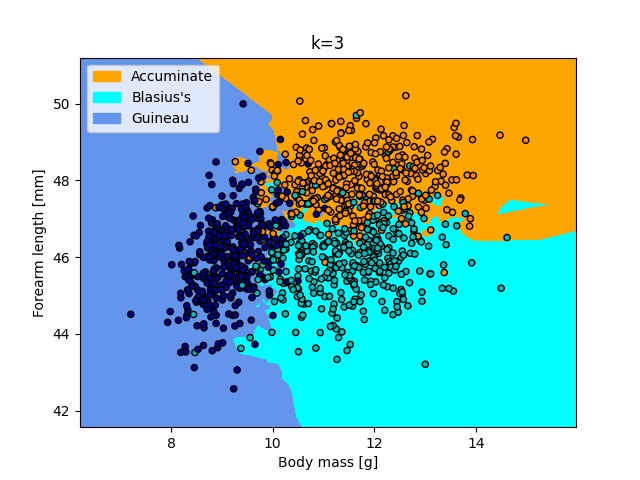
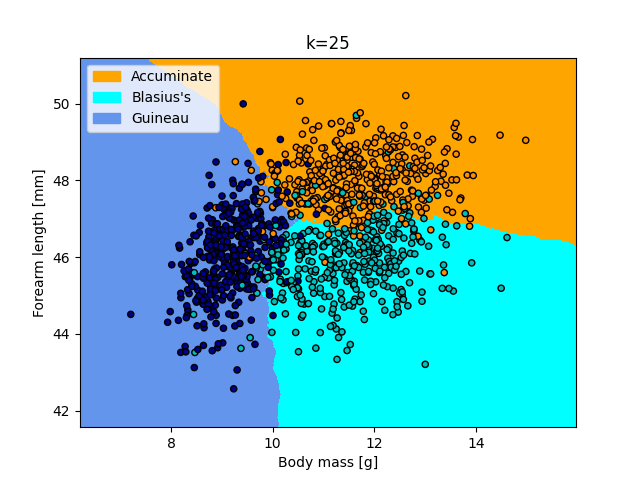
Below, the k-NN decision boundaries obtained with the bat training data are visualised for two distinct values of $k$. Based on the figures, which value of $k$ is most suitable?

k-NN decision boundaries using $k = 3$
k-NN decision boundaries using $k = 3$
k-NN decision boundaries using $k = 25$
k-NN decision boundaries using $k = 25$

Select $k$:


Question D: New Observation

One day, the research team gets a call from a fellow colleague that is currently on a research station not far from where the team operates. She has observed a horseshoe bat nearby the station and she can not decide what species it belongs to. Luckily, your model is ready for use. The bat in question has a forearm length of 44.5 mm and a body mass of 10.3 g.

Fill in the missing lines in the code below to predict the species of the newly observed bat. Specifically, you need to compute the distance between the input vector of the newly observed bat, and those of all the training data points, in order to determine which of the training data points that are the nearest neighbors. The common notion of distance (that is, the length of a straight line between two points) is in mathematical terms referred to as the Euclidean distance. To compute it in the code below, it is convenient to use the broadcasting feature of NumPy arrays and functions for computing the square (**2) and square root (np.sqrt) of all elements of an array, as well as summing (np.sum) the elements of an array. Remember from the NumPy introduction that the axis parameter can be used to sum the elements of an array along a certain axis.

Use the value of $k$ that you found to be suitable in the previous question. While the data we will work with here only has two attributes, the predict method (including the euclidean distance calculation) should be implemented to work for data with any number of attributes.


Question E: Test Accuracy

You have now used your model to predict the species of a bat, but how do you know if your model is trustworthy? To evaluate your k-NN model, you can make predictions for a full new set of observed bats, that have not been included in the model itself, and for which you already know the true species. This type of testing will give you an idea of how well the model is expected to perform when put in production. We will return to the process of model evaluation and study it in more detail in section 4, but it is useful to get acquainted with the idea already now.

Based on this idea, there are several evaluation metrics that you can use to evaluate your model. One commonly used evaluation metric is accuracy, which is equal to the proportion of correct predictions among the new set of observations $\left\{\mathbf{x}_i, y_i \right\}_{i=1}^{n_t}$.

Here, we have added a subscript $t$ on $n_t$ to indicate that this is the number of test data points. Recall that the indicator function $\mathbb{I}$ is equal to 1 if the statement is true, and zero otherwise.

Finalize the code below to calculate the accuracy of your model using the test dataset of the remaining 269 bat observations that were not used for training.


Conclusion

Well done, you have now implemented and evaluated a k-NN model for classification and used it to predict the species of a horseshoe bat! In the next example, you will see how the k-NN model can be applied to a regression task.

Linköping University
Department of Computer and Information Science
foundations-of-ml@ida.liu.se

This webpage contains the course materials for the course ETE370 Foundations of Machine Learning.
The content is licensed under Creative Commons Attribution 4.0 International.
Copyright © 2021, Joel Oskarsson, Amanda Olmin & Fredrik Lindsten