FOUNDATIONS OF MACHINE LEARNING
Course info
Course materials
FAQ
Course materials
/
Section
Penguins in Antarctica
Penguins are a group of birds located on the southern hemisphere and better adapted for swimming than for flying. Although there are close to 20 penguins species on the planet, you will in this problem classify the penguins from the three species found in the Palmer Penguins dataset, namely Adélie, Chinstrap and Gentoo penguins. The data was originally published in an article studying differences in physical attributes between sexes of several penguin species in Antarctica (Gorman et al., 2014) and consists of 344 observations in total.

For this exercise, the following penguin attributes will be considered:
- Species (Adélie/Chinstrap/Gentoo)
- Bill length [mm]
- Body mass [g]
- Flipper length [mm]
In python, the Palmer Penguins dataset can easily be accessed through the palmerpenguins library. For this exercise, we split the data into training and test sets. The training data, consisting of 274 observations, is shown in the figure below.
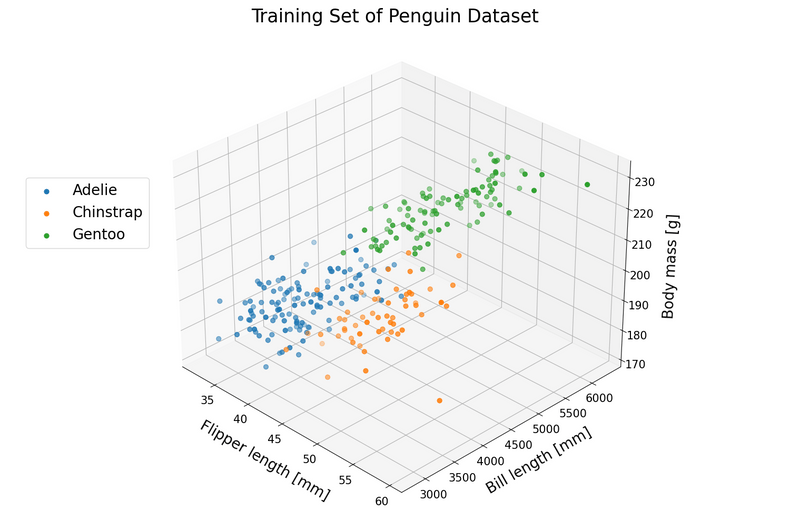
Your task is to build a logistic regression model that classifies the penguin species based on the remaining variables listed above.
You will not need to build the model from scratch, but will instead employ the LogisticRegression built-in classifier from the scikit-learn library.
Logistic regression
Logistic regression is introduced in chapter 3.2 of the course book. The logistic regression model can be seen as an extension of linear regression, where a transformation is added to the output to obtain predictions in the interval [0, 1]. For a classification problem with $M$ classes, we obtain the $m^{th}$ element in the output vector using a softmax function according to
The softmax function ensures that $g_m (\mathbf{x}) \in [0, 1]$ and that the elements of the output vector sum to one, i.e. $\sum_{j=1}^{M} g_j (\mathbf{x}) = 1$. In the light of this, we can interpret the output of a logistic regression model as a vector of probabilities over classes. That is, the model predicts the probability that an input $\mathbf{x}$ belongs to each of the $M$ classes such that $g_m (\mathbf{x}) = p(y=m \mid \mathbf{x})$.
To visualise the behaviour of a logistic regression model, we can look at a simple binary classification example where the input has dimension 1. We plot the probability $p(y=1\mid x)$ as predicted by the model and also include the data that was used to train the model. Since we know the true class of the training data points, the probability that they belong to class 1 is either 0 or 1.
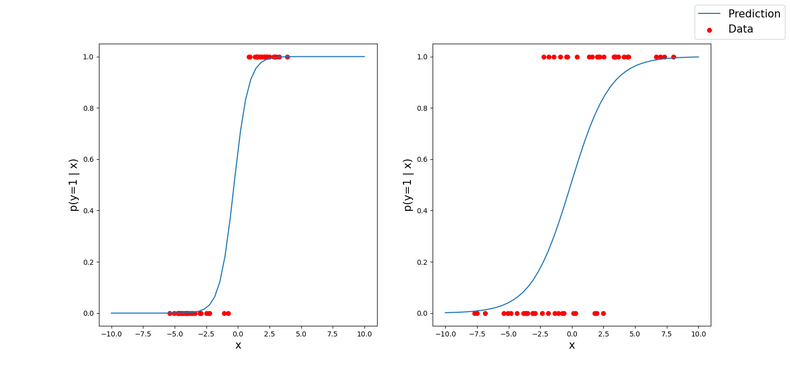
We can see that the model’s predictions follow an s-shaped curve. When the the training data points from the two classes are well separated, the curve is rather sharp (left figure). When there is a larger overlap between the classes (right figure), the model is more uncertain about where the true decision boundary lies and we obtain a flatter curve.
From the course book you have learned that we cannot find the parameters of a logistic regression model in closed form. Hence, you will need to use a numerical optimization method to
learn the parameters of the model. The scikit-learn LogisticRegression classifier uses an optimization algorithm called “LBFGS” as default. If you are interested, you can read more about
the LogisticRegression classifier and the optimization method by following this link,
or have a look at chapter 5 of the course book which gives an introduction to numerical optimization.
However, at this stage, it is okay if you do not fully understand how an optimization algorithm works under the hood. It is good to know that the aim of the optimization is to
find the model parameters that maximizes the data likelihood though.
Below, you find a code snippet that loads the penguin data, splits it into training and test sets and then uses the training data to find the parameters of a logistic regression model.
Fill in the empty parameters in the fit function and run the code to find your model parameters.
Note: the only function parameter that we have changed from its default value in the code is the max_iter parameter of the fit function, corresponding to the maximum number of
iterations that the algorithm will perform. An iteration, in this case, is an update of the model parameters in an attempt to find a maximum of the data likelihood.
By increasing the number of maximum iterations, we give the algorithm more time to find suitable model parameters. Feel free to play around with the other parameters of the functions used,
but make sure to head back to the original settings before submitting your answer.
The maximum likelihood approach
In the problem above, we found the parameters of the logistic regression model by maximizing the data likelihood. This means that we search for the parameters such that the probability (according to the model) of observing the data points in our training dataset is maximized.
As an example, consider the simple case of modeling the outcome of flipping a (possibly unfair) coin. Let $\theta$ denote the probability of flipping heads and, consequently, $1-\theta$ is the probability of getting tails. Suppose that you have flipped the coin 1000 times whereof 517 came up heads and the rest came up tails. An intuitive estimate of $\theta$, without knowing anything else about the coin, would be as the proportion of flips that came up heads: $\hat{\theta} = \frac{517}{1000} = 0.517$.
This estimate turns out to be the maximum likelhood solution. To formalize this mathematically, the objective is to maximize the likelihood $p(\mathbf{y}; \theta)$ of the observed data $\mathbf{y}$ (a vector of heads and tails) according to
We assume that each observation $y_i$ comes from the same probability distribution (a so called Bernoulli distribution), with parameter $\theta$ denoting the probability of $y_i = \text{heads}$. Furthermore, we assume that all the coin flips are independent, which means that the total probability of observing the $n$ values in the training dataset is equal to the product of all individual probabilities. That is, if $m$ out of $n$ flips came up heads (thus, $n-m$ came up tails), the data likelihood (= total probability of the observed data) is
For mathematical convenience and numerical stability, it is common to work with the log-likelihood
Since the natural logarithm is an increasing function, maximizing the log-likelihood also maximizes the original likelihood function. To find the parameter that maximizes the log-likelihood, we take the derivative with respect to $\theta$
Setting this derivative to zero and solving for $\theta$ yields $\hat{\theta} = \frac{m}{n}$. With $m=517$ and $n=1000$, we recover our intuitive estimate: $\hat{\theta} = \frac{517}{1000}$.
Training a classification model using the maximum likelihood principle follows the same idea. The only difference is that the output $y$ now depends on some fixed input $\mathbf{x}$ and we want to build a model for the conditional probability $p(y \mid \mathbf{x})$. For a parametric model, such as logistic regression, we can write this conditional probability as $p(y \mid \mathbf{x} ; \boldsymbol{\theta})$ where $\boldsymbol{\theta}$ denotes a vector of model parameters. Training the model then amounts to making it as likely as possible to observe the (known) training data outputs with respect to the model. As above, we assume that each observation $y_i$ only dependent on the corresponding input $\mathbf{x}_i$. The data likelihood then becomes
The logistic regression model, defined by the parameters $\boldsymbol{\theta}$, describes the relationship between the class $y$ and input $\mathbf{x}$. When we give a value $\mathbf{x}$ as input to the model, we obtain a probability vector corresponding to the parameters of a categorical distribution over $y$. Unlike the case with the coin flip, our model now describes a conditional distribution for any value of $\mathbf{x}$. As a result of this, and when the dimension of $\boldsymbol{\theta}$ grows, it is rarely the case that we can estimate $\boldsymbol{\theta}$ analytically as in the coin flip example. Therefore we resolve to numerical optimization methods for maximizing the data likelihood.
Evaluate your model by calculating the accuracy on the test data (hint: you can use the score function of your trained model).
If you plug in a penguin with a bill length of 45.22 mm, flipper length of 3701 mm and a body mass of 218.7 g into your logistic regression model, you should obtain a logit vector $\mathbf{z}=[-2.397, -0.106, 2.503]^\top$. Use a calculator or the code block below and the softmax function (Eq. 3.41 in the course book) to find the probability that the penguin is a Chinstrap penguin. Note: the species have been numerically encoded according to: 1=Adélie, 2=Chinstrap, 3=Gentoo.
Give your answer as a percentage with one decimal place.
Use your calculated probabilities to predict the species of the penguin from the previous question.
According to the model, the most likely species is:
Missing values
In this problem, we swept under the rug the fact that we excluded two observations from the penguin dataset in the code. The reason for doing so was that these two examples had missing values, meaning that one or more of the variable values were unknown. In reality, we might have wanted to use some method to account for or fill in the missing values. In that way, we could have included the observations in our dataset. You can read more about missing values in chapter 10.4 in the course book.
In this example, you have seen how you can transform the linear regression model into logistic regression—a model that can be used for solving classification problems. This was accomplished by applying a simple nonlinear transformation (the softmax function) to the model output. The transformation makes sure that we obtain reasonable model predictions; which in this case are probabilities and therefore should be in the range [0, 1].
As it turns out, the idea of combining (learnable) linear functions with (fixed) nonlinear transformations can be used to construct very flexible models, capable of capturing very complex relationships between input and output variables. We will return to this in section 5, when we introduce a type of parametric models known as neural networks.
Gorman, K. B., Williams, T. D., & Fraser, W. R. (2014). Ecological sexual dimorphism and environmental variability within a community of Antarctic penguins (genus Pygoscelis). PloS one, 9(3), e90081.
This webpage contains the course materials for the course ETE370 Foundations of Machine Learning.
The content is licensed under Creative Commons Attribution 4.0 International.
Copyright © 2021, Joel Oskarsson, Amanda Olmin & Fredrik Lindsten