The task of modeling a (possibly very complex) probability distribution $p(\mathbf{x})$ can be seen as one of the most fundamental challenges in machine learning. Most problems we are interested in one way or another boils down to modeling some distribution. It should then be of little surprise that the family of deep generative models, that offer methods for modeling even the most complex of distributions, have recieved much attention. One application of these models that consistently manages to amaze researchers and the public alike is image generation. Look for example at the images below:

Despite looking very realistic, the people and animals in these images are not real. The images have been generated by deep generative models trained on large datasets.

While these methods still see limited use in industry today, they are very hot research topics and will surely continue to make their way into applications in the future. Additionally, since the task of modeling distributions is so fundamental, many of the ideas used in deep generative models are useful also in other areas of machine learning. For these reasons it is good to have a general idea about what deep generative models are and what different types of models that exist.

In this section we aim to initially deepen our understanding of how deep generative models work. We will look at examples at how a very simple distribution combined with a complex transformation can be used to model more complex distributions. To recap the different types of deep generative models we will also ask some questions related to Normalizing Flows and Generative Adversarial Networks.

One way to model a complex distribution $p(\mathbf{x})$ is through a combination of a simple distribution and a complicated transformation. We will here give a short recap on this idea, since it is fundamental to understanding deep generative models.

Consider first a simple distribution $p_{\mathbf{z}}(\mathbf{z})$, for example (and the typical choice in practice) a standard Gaussian $\mathcal{N}(0, I)$. If we draw a sample $\mathbf{z}$ from this distribution and propagate it through some function $f_\theta$, we will get a new variable $\mathbf{x} = f_\theta(\mathbf{z})$. Importantly, the distribution of $\mathbf{x}$ is no longer a standard Gaussian. Instead the distribution of $\mathbf{x}$ depends on the function $f_\theta$.

For example, if $f_\theta(\mathbf{z}) = 2\mathbf{z} + 1$ then $\mathbf{x} = 2\mathbf{z} + 1$ follows the distribution $\mathcal{N}(1, 4I)$. This is however still Gaussian. If we consider a more complicated, non-linear transformation we can also move outside this class of distributions. If we choose $f_\theta(\mathbf{z}) = \exp(\mathbf{z})$, then $\mathbf{x}$ will no longer be Gaussian (the distribution of $\mathbf{x}$ would be what is called a multivariate log-normal distribution). Furthermore, if we chain many simple transformations together (like the layers in a neural network) it is possible to make the distribution of $\mathbf{x}$ very complex.

Before we continue our discussion about specific types of deep generative models, let us look at some additional examples of transformations $f_\theta$.

The plot below shows probability densities of the two-dimensional random variables $\mathbf{z}$ and $\mathbf{x} = f_\theta(\mathbf{z})$. The left plot shows $p_{\mathbf{z}}(\mathbf{z})$, a standard Gaussian. The right plot shows $p(\mathbf{x})$, the probability density function of the transformed random variable $\mathbf{x}$. Your task is to figure out what transformation $f_\theta$ the plots correspond to. Put differently, which $f_\theta$ transforms the Gaussian distribution to the left to the distribution depicted to the right?

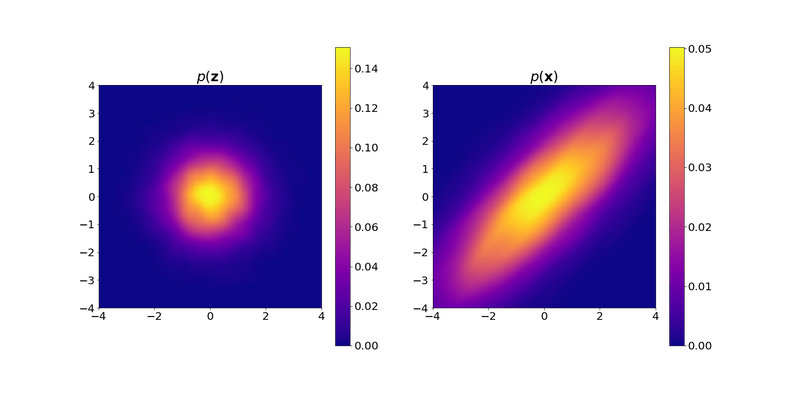
Remark: If you wonder why the density plots are a bit “ragged”, it is because they are approximated based on samples drawn from the corresponding distributions. Specifically, the density is computed using kernel density estimation based on the generated samples. The left plot is based on samples drawn from a standard Gaussian distribution, and the right plot on the same samples but propagated through the function $f_\theta$.

Using the same setting as above, which transformation $f_\theta$ is depicted in the plot?

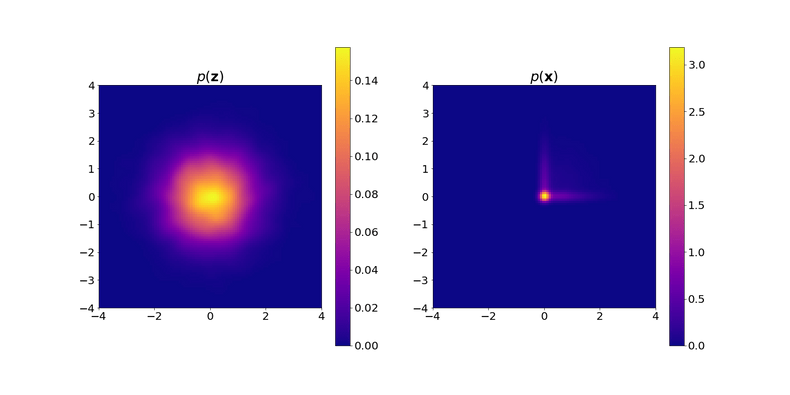
Using the same setting as above, which transformation $f_\theta$ is depicted in the plot?

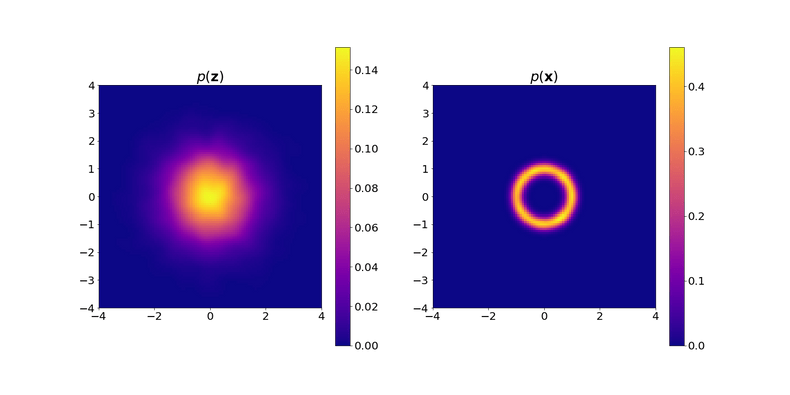
Some deep generative models, like Normalizing Flows, rely on invertible transformations $f_\theta$. They require that an inverse exists so that one can map $\mathbf{z} = f_\theta^{-1}(\mathbf{x})$. Out of the three transformations depicted in the plots in Question A-C, which of them is invertible?

$f_\theta$ from Question A

$f_\theta$ from Question B

$f_\theta$ from Question C

As we can see, the distribution of $\mathbf{x}$ depends on the choice of transformation $f_\theta$. If we additionally define this transformation using a parametric model with parameters $\theta$ the distribution of $\mathbf{x}$ will in turn be defined by $\theta$. This means that, if we can find a way to learn such a model by optimizing $\theta$, then we can learn models for very complex probability distributions. Specifically, we can optimzie $\theta$ based on the criterion that the distribution of the generated samples $\mathbf{x} = f_\theta(\mathbf{z})$ where $\mathbf{z} \sim N(0,I)$, should match the distribution of some training dataset. If this is the case, we have effectively learned a generative model that is capable of producing synthetic data samples that are similar (in distribution) to the training data. By choosing $f_\theta$ as a deep neural network, we get a very powerful transformation.

The question remains, how do we train such a model to find $\theta$ that makes the distribution of $\mathbf{x}$ match our data? This is where the difficulty of deep generative models really shows. We have devised a nice scheme for sampling $\mathbf{x}$, but said nothing about the explicit form of the distribution $p(\mathbf{x})$.

In the course book two different types of deep generative models are introduced, Normalizing Flows and Generative Adversarial Networks. These offer two different solutions to the training problem. In the following exercises we want you to reflect on how these models are trained and what are their limitations. Feel free to revisit chapter 10.3 in the course book to refresh your memory.

Which of the following statements about Normalizing Flows are true?

Normalizing Flows require that the transformation $f_\theta$ only takes positive values.

Normalizing Flows require that the transformation $f_\theta$ is invertible.

Normalizing Flows require that the dimension of $\mathbf{z}$ is the same as the dimension of $\mathbf{x}$.

Normalizing Flows can only model Gaussian distributions.

For Normalizing Flows, the likelihood function can be explicitly written down and optimized.

Which of the following statements about Generative Adversarial Networks (GANs) are true?

GANs require sampling from the model distribution $p(\mathbf{x} | \theta)$ during training.

Training a GAN involves propagating the data through a critic network.

Sampling from a GAN involves propagating the data through a critic network.

GANs require that the dimension of $\mathbf{z}$ is the same as the dimension of $\mathbf{x}$.

For GANs, the likelihood function can be explicitly written down and optimized.

We have earlier seen how deep generative models can be used for two-dimensional data. Hopefully this has showcased how these models work on a basic level. It might still seem a bit mysterious how we can get from modeling these distributions to generating realistic-looking images, a task where deep generative models have set a completely new standard on what is possible.

However, in principle, generating an image is really not that different from generating a two-dimensional sample. It is just the dimensionality that differs. If we for example work with 64$\times$64 pixel grayscale images, this means that $\mathbf{x}$ is 4096-dimensional. Generating such images using a deep generative model could be done in the same way as described earlier, by sampling $\mathbf{z}$ and propagating it through a complex transformation to get the high-dimensional $\mathbf{x}$ as output. The image distribution being modeled is over a 4096-dimensional space and is incredibly complex. This requires a very flexible and powerful transformation in order to properly learn the distribution. Very deep neural networks have shown to be capable of this. Of course, for images one can also make use of CNNs in order to easier handle the high dimensionality of the data. It is also important to keep in mind that it is not enough to just specify such a model, but we also need to have the data to train it. Training deep generative models on high-dimensional data such as images requires very large datasets.

Research in the area of deep generative models has made rapid progression in few years. Take the image generation task as an example. Initial models, such as the ones introduced in the original GAN paper by Goodfellow et al., (2014), generated blurry-looking images often featuring non-realistic artifacts. The models of today can generate images that are almost indistinguishable from real photos. A great example of this can be found on the website thispersondoesnotexist.com. The people in the images on the site are not real, but generated by a deep generative model called StyleGAN (Karras et al., 2020). Similar webpages exist also for cats and horses, with images generated by the same type of model. Recently a class of models called Diffusion models have pushed the state of the art even further, generating highly diverse and realistic images (Ho et al., 2020). Diffusion models like Dall-E 2 (Ramesh et al., 2022) and Imagen (Saharia et al., 2022) have recieved much attention due to their ability to generate realistic images based on a specific text prompt. Also Diffusion models are based on the key idea of transforming a simple distribution to something much more complex by applying a sequence of transformations.

While image generation has been the standard task driving much of the research, the actual use-cases for image generators might seem somewhat narrow. Of course deep generative models can be used to generate all kinds of data, for example:

• Text (have a look at the subsection on Generative Language Models if this seems interesting!)
• Music and Speech (van den Oord et al., 2016)
• Videos (Tulyakov et al., 2018)
• Molecules (Sanchez-Lengeling & Aspuru-Guzik, 2018)
• Community-graphs (Liu et al., 2019)

We have yet to see the impact of this powerful technology on various application fields.

The possibility to generate new data that is realistic enough to fool humans does come with a number of societal implications. While crafting of realistic fake photos and videos is not new, deep generative models both lower the barrier of entry to these techniques and achieve things not previously possible. Just generating completely new fake samples might not be that problematic, but more severe ethical concerns emerge when generative models are used to alter existing media. Several techniques have already been developed where deep generative models can be used to change photos and videos in highly realistic ways. The face of a person could for example be overlayed realistically on an actor or a sound clip could be generated using the voice of a real person. These techniques are often referred to as “Deepfakes”. There are many concerns related to the use of Deepfakes, in particular in connection with political disinformation and fraud. Generated Deepfake video and audio of politicians could be used as a very powerful weapon to try to manipulate political processes.

We should of course point out that there are two sides of the coin and other applications of deep generative models have the potential to be beneficial to society. In the medical sciences gathering large datasets for use in research can be a challenge, partly due to ethical concerns and heavy regulations on patient data. Deep generative models offer the possibility to generate realistic patient data, such as fMRI images of the brain, for patients that do not actually exist (Gu et al., 2019). This could help speed up medical research, in particular in combination with other machine learning techniques. Also in content creation for media and movies deep generative models can offer a fast way to create realistic and impressive pieces. Some models also allow a user to tweak generated samples, making the model a powerful tool for human creativity (Perarnau et al., 2016).

As we can see, the potential use cases for deep generative models are many and some come with heavy ethical implications. We have here covered GANs, Normalizing Flows and briefly mentioned Diffusion models, but the research in this area is moving quickly and we will likely soon see these models being developed further and new types of models emerge. The core ideas behind these models do however stay relevant and find their ways into many areas of modern machine learning.